GCN(Graph Convolutional Network)的理解

在深度學習領域的人，對捲積(Convolution)應該都不陌生，但不一定聽說過圖(Graph)也可以做Convolution。這篇文章對GCN(Graph Convolutional Network)做了概略的介紹。

CNN的捲積不是數學定義上的連續捲積，而是一種定義的離散捲積。我們用這種捲積來處理圖像(image)，從圖像中提取特徵，並且透過神經網路來學習捲積的權重(weight)。以下所稱的捲積都是指這種局部的離散捲積。

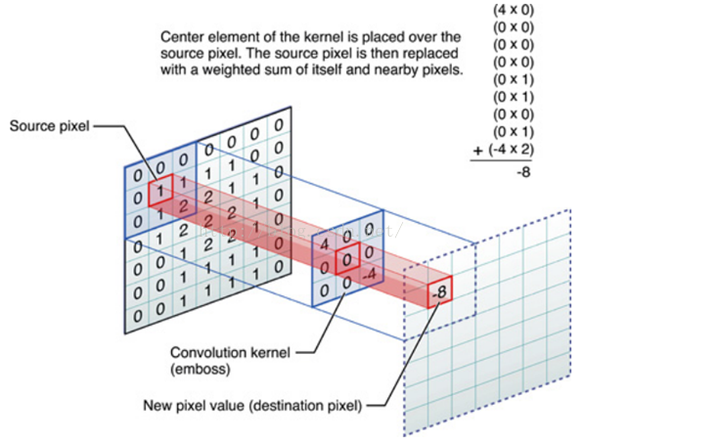
CNN捲積有一些特性，

(1)平移不變性(shift-invariance) (2)局部性(local connectivity) (3)多尺度(multi-scale)

這些特性，暫且把它們稱作組合性(Compositionality)，讓CNN捲積只能處理在歐幾里德空間(Euclidean Structure)的數據。

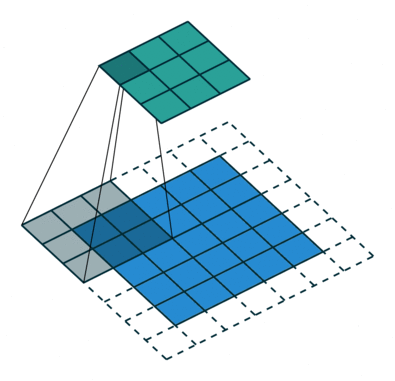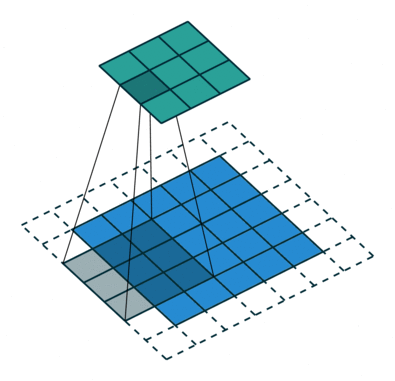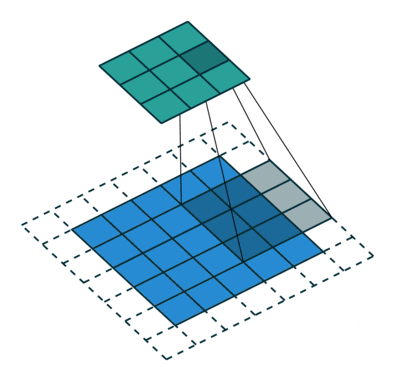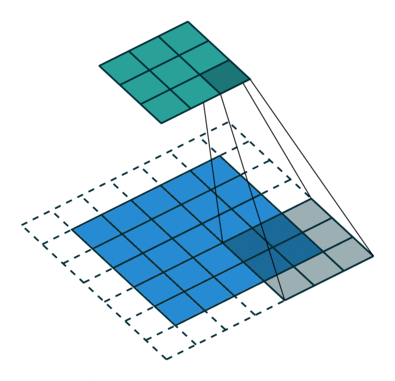
什麼數據是Euclidean Structure的數據呢？最經典的就是影像(image)，影片(video)和音頻(speech/voice)，自然語言文本(text)透過特殊處理，也可以固定維度，投影到歐幾里德空間來操作。

然而，有一些數據結構是Non-Euclidean的，例如:

生物/化學分子 Chemical/Biological Graphs

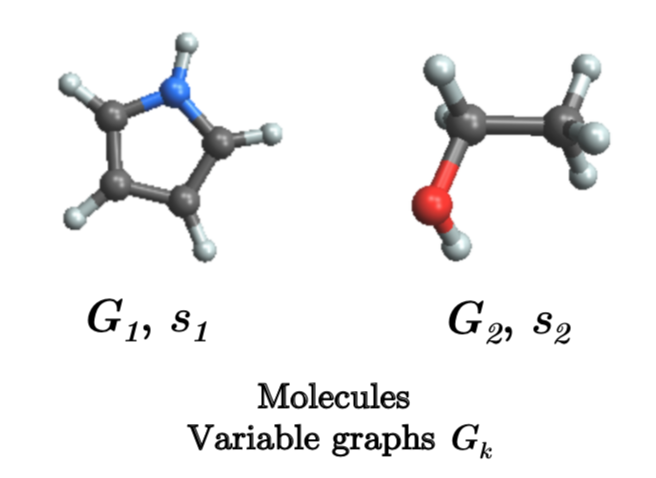
Citation Networks / Social Networks

Unstructured Graphs: 例如3D點雲, 或者是半監督學習

Non-Euclidean的數據，大致上可以當作圖(Graph)來理解。也就是可以理解成$G=(V,E)$，由頂點(vertex)和邊(edge)所構成的一種資料格式。

Euclidean數據可以當作是Non-Euclidean的一種特例。因此對Non-Euclidean理解和處理，可以在Euclidean數據上通用，這就是為什麼Non-Euclidean數據的表示法學習有其重要性。

對2D Convolution來說，Graph Convolution的想法來自於把在圖像域(image domain)運作得很好的2D捲積神經網路方法，拿到圖域(graph domain)來使用。

要了解圖的Convolution，要先了解Convolution本質上是一種aggregation操作，它是一種局部加權平均的運算。

對圖的頂點(vertex)來說，局部指的是它的鄰居，而它的鄰居由邊(edge)的存在與否，綜合邊的權重(weight)大小去定義。簡單起見，把有邊(edge)的權重都定為$1$，沒邊(edge)的權重都定為$0$。

為了探討圖的性質，我們用度矩陣(degree matrix)$D$ 和 鄰居矩陣(adjacency matrix)$A$來表示一個圖。度矩陣是一個對角矩陣(diagonal matrix)，度矩陣對角線上的值就是該頂點連接著幾條邊，也就是鄰居矩陣的列和。

假如是無向圖，鄰居矩陣是對稱矩陣(symmetric matrix)。

1 2	import numpy as np D = np.sum(A, 1)

另外圖論(graph theory)還定義一個東西叫做Laplacian Matrix $L$，它最簡單的定義是$D-A$。在數學及物理中，Laplacian或稱Laplace operator(拉普拉斯算子)是歐幾里得空間中的一個函數的梯度的散度給出的微分算子，通常寫成 $\Delta$、$\nabla^2$ 或 $\nabla \cdot \nabla$。可以粗糙的視為歐幾里得空間中二次微分操作。

Laplacian物理上的解釋可以是能量的流失或是物質擴散，放在圖論上來說，即是該頂點信息(message)傳播(propagation)。

圖卷積神經網路(GCN)的單層操作，則可以(但不一定要)定義成： \[Y=LX\]

因為圖的Laplacian Matrix最簡單的定義是$L=D-A$： \[Y=LX=DX-AX\]

對單一節點來說，式中的 $AX$ 可以視為本次操作(每單位時間)鄰居預計要從我身上拿走的訊息量。 $DX$ 可以視為是本次操作每個節點尚未進行傳播前，本來擁有的訊息量，即是上次操作(上一個單位時間)每個頂點從它的鄰居頂點取得的訊息量。兩者相減，就是本次操作後訊息傳播的狀況。

我們用程式碼來了解一下圖的訊息傳遞：

# 定義鄰居矩陣A，故意使它不對稱，有向圖比較容易看到訊息傳遞的狀況
import numpy as np

A = np.matrix([
    [0, 1, 0, 0],
    [0, 0, 1, 1], 
    [0, 0, 0, 0],
    [1, 0, 1, 0]],
    dtype=float
)

# 畫圖程式(optional)
import networkx as nx
import matplotlib.pyplot as plt
G=nx.DiGraph(A)
nx.draw(G, with_labels=True)
plt.show()

這個有向圖可以理解為，每次的$L$操作，每個節點會依照箭頭指出的方向去提供每個鄰居節點它所要求攜帶的訊息。

# 定義初始特徵
X = np.matrix([[ 100., -100.],
                [ 1., -1.],
                [ 2., -2.],
                [ 3., -3.]])

A * X

#輸出：
matrix([[   1.,   -1.],
        [   5.,   -5.],
        [   0.,    0.],
        [ 102., -102.]])

從以上例子就可以明顯看出，因為label=3的節點提供訊息給label=0和label=2的節點，結果得到一個很大的訊息更新。

1
2
3

D = np.diag(np.array(np.sum(A, 1)).flatten())
L = D-A
L*X

#輸出：
matrix([[ 99., -99.],
        [ -3.,   3.],
        [  0.,   0.],
        [-96.,  96.]])

結果label=3的節點更新完後，有了很大的變化。

我們這時候應該也發現了一些問題。由於圖中沒有自環，訊息只能被鄰居不斷取走，而沒有因應自身訊息做調整。這就像是預估一個人薪水多高時，只考慮他的朋友薪水多高，而沒有把該人的自身條件考慮進去，顯然不太合理。因此，因應任務需要，可以考慮增加自環。

\[\hat{A} = A+I\]

# 增加自環
I = np.diag([1]*A.shape[0])
A_hat = A + I
A_hat

#輸出：
matrix([[1., 1., 0., 0.],
        [0., 1., 1., 1.],
        [0., 0., 1., 0.],
        [1., 0., 1., 1.]])

A_hat * X

#輸出：
matrix([[ 101., -101.],
        [   6.,   -6.],
        [   2.,   -2.],
        [ 105., -105.]])

1
2
3

D_hat = np.diag(np.array(np.sum(A, 1)).flatten())
L_hat = D_hat-A_hat
L_hat*X

#輸出：
matrix([[ -1.,   1.],
        [ -4.,   4.],
        [ -2.,   2.],
        [-99.,  99.]])

以上的傳播矩陣，不管是$A$還是$\hat{A}$還是$L$，與convolution相似的地方在於，它們都是一種局部的aggregation操作。然而，convolution的局部連接數是固定的，這裡卻不是這樣，每個頂點鄰居數目可能都不同。

所以，不管是$A$還是$\hat{A}$還是$L$，都還需要進行歸一化處理。以免偏好鄰居較多的節點，讓鄰居較多的節點傳播比較多的訊息量。歸一化處理的方法有兩種：(1)算術平均(2)幾何平均

於是多定義了兩種Laplacian Matrix (1)算術平均 \[L^{rw}=D^{-1}L\] (2)幾何平均 \[L^{sym}=D^{-0.5}LD^{-0.5}\]

其中，幾何平均受極端值影響較小，$L^{sym}$是GCN中較為常用的 Laplacian Matrix 。

故，圖卷積神經網路(GCN)的單層操作，也可以(但不一定要)定義成： \[Y=L^{sym}X\]

Eigendecomposition / Spectral decomposition of Laplacian Matrix

假設為無向圖，此時$L^{sym}$ (以下簡稱$L$) 是可以被對角化的 (原因不詳述)

$L= U\left(\begin{matrix}\lambda_1 & \\&\ddots \\ &&\lambda_n \end{matrix}\right) U^{-1}$

由於$U$是正交矩陣，$UU^T=I$，$U^T=U^{-1}$

$L= U\left(\begin{matrix}\lambda_1 & \\&\ddots \\ &&\lambda_n \end{matrix}\right) U^{T}$

其中，$U$是已知的，$\lambda_l$ 特徵值是未知要求取的。但我們並不直接去求或是去優化$\lambda_l$ 。

對一個捲積函數 $h$ 而言，可以用傅立葉轉換的卷積定理 $(f*h)_G=U((U^Th)\odot(U^Tf)) \qquad(2)$

去證明(原因不詳述)，捲積後的結果為：

$(f*h)_G= U\left(\begin{matrix}\hat h(\lambda_1) & \\&\ddots \\ &&\hat h(\lambda_n) \end{matrix}\right) U^Tf \qquad(1)$

其中$\hat{h}(\lambda_{l})$要設計成:

$\hat{h}(\lambda_l)=\sum_{i=1}^{N}{h(i) u_l^*(i)}$ 其中$u^{*}$是傅立葉轉換正交特徵向量的共軛轉置

第一代GCN

Spectral Networks and Locally Connected Networks on Graphs(2013)

直接令 $\theta_l=\hat{h}(\lambda_{l})$

GCN的單層操作:

$y_{output}=\sigma \left(U g_\theta(\Lambda) U^T x \right) \qquad(3)$ $g_\theta(\Lambda)=\left(\begin{matrix}\theta_1 &\\&\ddots \\ &&\theta_n \end{matrix}\right)$

第一代圖捲積跟一般CNN卷積的差異：

卷積核(kernel)只在主對角線上，並不需要是二維的，卷積核個數與頂點數(n)相同
卷積核(kernel)在主對角線上的矩陣需要經過離散傅立葉矩陣轉換($U$,$U^T$)

第二代GCN

Convolutional Neural Networks on Graphs with Fast Localized Spectral Filtering(2016)

設計： $\hat{h}(\lambda_{l})$= $\sum_{j=0}^K \alpha_j \lambda^j_l$ K是K-hop neighbor

可以導出GCN的單層操作（推導過程略）: $y_{output}=\sigma \left( \sum_{j=0}^K \alpha_j L^j x \right) \qquad(5)$ 卷積核(kernel)是$\alpha_j$

第二代圖捲積跟第一代圖捲積的差異：

第一代沒有局部性，卷積核個數與頂點數(n)相同，第二代只有K個參數，計算複雜度降低很多
第一代每次向前傳播都要計算一次 $U\ diag(\theta)\ U^T$ 三者的乘積，第二代直接拿$L$乘上$\alpha_j$，計算簡單一些，但複雜度仍是$O(n^2)$
第二代有Parameter Sharing的部份

對GCN的介紹暫時到這邊，有空再來分享paper和程式碼。實際上程式碼並沒有理論來的那麼複雜，用numpy自己刻一個是絕對可行的，假如用deep learning套件，實際上也只有用到fc layer。基於PyTorch有非常好用且完整的套件torch_geometric，雖無法handle大圖，但拿來上手可以很快進入狀況。

轉載請附上來源連結

Reference: